在PyTorch中计算图的特点可总结如下:
- autograd根据用户对variable的操作构建其计算图。对变量的操作抽象为
Function。 - 对于那些不是任何函数(Function)的输出,由用户创建的节点称为叶子节点,叶子节点的
grad_fn为None。叶子节点中需要求导的variable,具有AccumulateGrad标识,因其梯度是累加的。 - variable默认是不需要求导的,即
requires_grad属性默认为False,如果某一个节点requires_grad被设置为True,那么所有依赖它的节点requires_grad都为True。 - variable的
volatile属性默认为False,如果某一个variable的volatile属性被设为True,那么所有依赖它的节点volatile属性都为True。volatile属性为True的节点不会求导,volatile的优先级比requires_grad高。 - 多次反向传播时,梯度是累加的。反向传播的中间缓存会被清空,为进行多次反向传播需指定
retain_graph=True来保存这些缓存。 - 非叶子节点的梯度计算完之后即被清空,可以使用
autograd.grad或hook技术获取非叶子节点的值。 - variable的grad与data形状一致,应避免直接修改variable.data,因为对data的直接操作无法利用autograd进行反向传播
- 反向传播函数
backward的参数grad_variables可以看成链式求导的中间结果,如果是标量,可以省略,默认为1 - PyTorch采用动态图设计,可以很方便地查看中间层的输出,动态的设计计算图结构。
Variable类和计算图
简单的建立一个计算图,便于理解几个相关知识点:
-
requires_grad 是否要求导数,默认False,叶节点指定True后,依赖节点都被置为True
-
.backward() 根Variable的方法会反向求解叶Variable的梯度
-
.backward()方法grad_variable参数 形状与根Variable一致,非标量Variable反向传播方向指定
-
叶节点 由用户创建的计算图Variable对象,反向传播后会保留梯度grad数值,其他Variable会清空为None
-
grad_fn 指向创建Tensor的Function,如果某一个对象由用户创建,则指向None
-
.is_leaf 是否是叶节点
-
.grad_fn.next_functions 本节点接收的上级节点的grad_fn
-
.volatile 是否处于推理模式
import torch as tfrom torch.autograd import Variable as Va = V(t.ones(3,4),requires_grad=True)b = V(t.zeros(3,4))c = a.add(b)d = c.sum()d.backward()# 虽然没有要求cd的梯度,但是cd依赖于a,所以a要求求导则cd梯度属性会被默认置为Trueprint(a.requires_grad, b.requires_grad, c.requires_grad,d.requires_grad)# 叶节点(由用户创建)的grad_fn指向Noneprint(a.is_leaf, b.is_leaf, c.is_leaf,d.is_leaf)# 中间节点虽然要求求梯度,但是由于不是叶节点,其梯度不会保留,所以仍然是Noneprint(a.grad,b.grad,c.grad,d.grad)
True False True TrueTrue True False FalseVariable containing: 1 1 1 1 1 1 1 1 1 1 1 1[torch.FloatTensor of size 3x4] None None None
print('\n',a.grad_fn,'\n',b.grad_fn,'\n',c.grad_fn,'\n',d.grad_fn)
模拟一个简单的反向传播:
def f(x): """x^2 * e^x""" y = x**2 * t.exp(x) return ydef gradf(x): """2*x*e^x + x^2*e^x""" dx = 2*x*t.exp(x) + x**2*t.exp(x) return dxx = V(t.randn(3,4), requires_grad=True)y = f(x)y.backward(t.ones(y.size()))print(x.grad)print(gradf(x))
Variable containing: -0.3315 3.5068 -0.1079 -0.4308 -0.1202 -0.4529 -0.1873 0.6514 0.2343 0.1050 0.1223 15.9192[torch.FloatTensor of size 3x4]Variable containing: -0.3315 3.5068 -0.1079 -0.4308 -0.1202 -0.4529 -0.1873 0.6514 0.2343 0.1050 0.1223 15.9192[torch.FloatTensor of size 3x4]
结果一致。
.grad_fn.next_functions
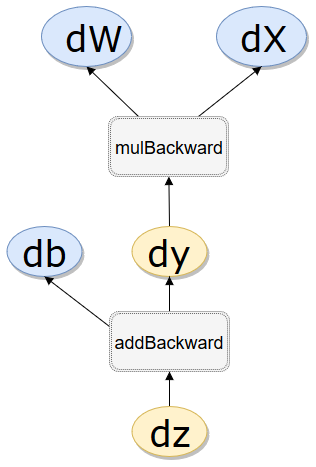
x = V(t.ones(1))w = V(t.rand(1),requires_grad=True)b = V(t.rand(1),requires_grad=True)y = w.mul(x)z = y.add(b)print(x.is_leaf,w.is_leaf,b.is_leaf,y.is_leaf,z.is_leaf)print(x.requires_grad,w.requires_grad,b.requires_grad,y.requires_grad,z.requires_grad)print(x.grad_fn,w.grad_fn,b.grad_fn,y.grad_fn,z.grad_fn)# grad_fn.next_functions# grad_fn.next_functions代表了本节点的输入节点信息,grad_fn表示了本节点的输出信息# 叶子结点grad_fn为None,没有next_functions,但是间接查询到AccumulateGrad object表示该叶子节点# 接受梯度更新,查询到None表示不接受更新print(y.grad_fn.next_functions,z.grad_fn.next_functions)print(z.grad_fn.next_functions[0][0]==y.grad_fn)print(z.grad_fn.next_functions[0][0],y.grad_fn)
.volatile.is_leaf True True True False False .requires_gradFalse True True True True .grad_fnNone None None.grad_fn.next_functions(( , 0), (None, 0)) (( , 0), ( , 0)) z.grad_fn.next_functions[0][0]==y.grad_fn Truez.grad_fn.next_functions[0][0],y.grad_fn
# volatile# 节省显存提高效用的参数volatile,也会作用于依赖路径全部的Variable上,且优先级高于requires_grad,# 这样我们在实际设计网络时不必修改其他叶子结点的requires_grad属性,只要将输入叶子volatile=True即可x = V(t.ones(1),volatile=True)w = V(t.rand(1),requires_grad=True)y = w.mul(x)print(x.requires_grad,w.requires_grad,y.requires_grad)print(x.volatile,w.volatile,y.volatile)
False True FalseTrue False True
附录、Variable类源码简介
class Variable(_C._VariableBase): """ Attributes: data: 任意类型的封装好的张量。 grad: 保存与data类型和位置相匹配的梯度,此属性难以分配并且不能重新分配。 requires_grad: 标记变量是否已经由一个需要调用到此变量的子图创建的bool值。只能在叶子变量上进行修改。 volatile: 标记变量是否能在推理模式下应用(如不保存历史记录)的bool值。只能在叶变量上更改。 is_leaf: 标记变量是否是图叶子(如由用户创建的变量)的bool值. grad_fn: Gradient function graph trace. Parameters: data (any tensor class): 要包装的张量. requires_grad (bool): bool型的标记值. **Keyword only.** volatile (bool): bool型的标记值. **Keyword only.** """ def backward(self, gradient=None, retain_graph=None, create_graph=None, retain_variables=None): """计算关于当前图叶子变量的梯度,图使用链式法则导致分化 如果Variable是一个标量(例如它包含一个单元素数据),你无需对backward()指定任何参数 如果变量不是标量(包含多个元素数据的矢量)且需要梯度,函数需要额外的梯度; 需要指定一个和tensor的形状匹配的grad_output参数(y在指定方向投影对x的导数); 可以是一个类型和位置相匹配且包含与自身相关的不同函数梯度的张量。 函数在叶子上累积梯度,调用前需要对该叶子进行清零。 Arguments: grad_variables (Tensor, Variable or None): 变量的梯度,如果是一个张量,除非“create_graph”是True,否则会自动转换成volatile型的变量。 可以为标量变量或不需要grad的值指定None值。如果None值可接受,则此参数可选。 retain_graph (bool, optional): 如果为False,用来计算梯度的图将被释放。 在几乎所有情况下,将此选项设置为True不是必需的,通常可以以更有效的方式解决。 默认值为create_graph的值。 create_graph (bool, optional): 为True时,会构造一个导数的图,用来计算出更高阶导数结果。 默认为False,除非``gradient``是一个volatile变量。 """ torch.autograd.backward(self, gradient, retain_graph, create_graph, retain_variables) def register_hook(self, hook): """Registers a backward hook. 每当与variable相关的梯度被计算时调用hook,hook的申明:hook(grad)->Variable or None 不能对hook的参数进行修改,但可以选择性地返回一个新的梯度以用在`grad`的相应位置。 函数返回一个handle,其``handle.remove()``方法用于将hook从模块中移除。 Example: >>> v = Variable(torch.Tensor([0, 0, 0]), requires_grad=True) >>> h = v.register_hook(lambda grad: grad * 2) # double the gradient >>> v.backward(torch.Tensor([1, 1, 1])) >>> v.grad.data 2 2 2 [torch.FloatTensor of size 3] >>> h.remove() # removes the hook """ if self.volatile: raise RuntimeError("cannot register a hook on a volatile variable") if not self.requires_grad: raise RuntimeError("cannot register a hook on a variable that " "doesn't require gradient") if self._backward_hooks is None: self._backward_hooks = OrderedDict() if self.grad_fn is not None: self.grad_fn._register_hook_dict(self) handle = hooks.RemovableHandle(self._backward_hooks) self._backward_hooks[handle.id] = hook return handle def reinforce(self, reward): """Registers a reward obtained as a result of a stochastic process. 区分随机节点需要为他们提供reward值。如果图表中包含任何的随机操作,都应该在其输出上调用此函数,否则会出现错误。 Parameters: reward(Tensor): 带有每个元素奖赏的张量,必须与Variable数据的设备位置和形状相匹配。 """ if not isinstance(self.grad_fn, StochasticFunction): raise RuntimeError("reinforce() can be only called on outputs " "of stochastic functions") self.grad_fn._reinforce(reward) def detach(self): """返回一个从当前图分离出来的心变量。 结果不需要梯度,如果输入是volatile,则输出也是volatile。 .. 注意:: 返回变量使用与原始变量相同的数据张量,并且可以看到其中任何一个的就地修改,并且可能会触发正确性检查中的错误。 """ result = NoGrad()(self) # this is needed, because it merges version counters result._grad_fn = None return result def detach_(self): """从创建它的图中分离出变量并作为该图的一个叶子""" self._grad_fn = None self.requires_grad = False def retain_grad(self): """Enables .grad attribute for non-leaf Variables.""" if self.grad_fn is None: # no-op for leaves return if not self.requires_grad: raise RuntimeError("can't retain_grad on Variable that has requires_grad=False") if hasattr(self, 'retains_grad'): return weak_self = weakref.ref(self) def retain_grad_hook(grad): var = weak_self() if var is None: return if var._grad is None: var._grad = grad.clone() else: var._grad = var._grad + grad self.register_hook(retain_grad_hook) self.retains_grad = True